Công thức tính diện tích mặt cầu ngoại tiếp hình chóp

1. Định nghĩa mặt cầu

Tập hợp các điểm M trong không gian cách điểm O cố định một khoảng R (R>0) không đổi gọi là mặt cầu có tâm O và bán khính bằng R.

Mặt cầu như thế thường được kí hiệu là S(O ; R).

Cho mặt cầu tâm o bán kính r và M là một điểm bất kì trong không gian.

– Nếu OM = r thì ta nói điểm M nằm trên mặt cầu S(O;r).
– Nếu OM<r thì ta nói điểm M nằm trong mặt cầu S(O;r)
– Nếu OM > r thì ta nói điểm M nằm ngoài mặt cầu S(O;r)

2. Giao của mặt cầu và mặt phẳng

Cho mặt cầu S (O;r) và mặt phẳng (P). H là hình chiếu vuông góc của O lên mặt phẳng (P). Khi đó OH =h là khoảng cách từ tâm O của mặt cầu tới mặt phẳng (P).

Ta có trường hợp:

– Nếu h>r thì mặt phẳng (P) không cắt mặt cầu;
– Nếu h=r thì mặt phẳng (P) tiếp xúc với mặt cầu tại điểm H. Ta có OH vuông góc với (P).
– Nếu h<r thì mặt phẳng (P) cắt mặt cầu theo đường tròn có bán kính … và có tâm là điểm H.

Khi h=0 thì mặt phẳng (P) cắt mặt cầu theo một đường tròn lớn có bán kính.

3. Giao của mặt cầu với đường thẳng, tiếp tuyến của mặt cầu.

Cho mặt cầu S (O;r) và đường thẳng

1. Trường hợpđi qua tâm O của mặt cầu thìcắt mặt cầu tại hai điểm A, B với AB =2r.

2. Trường hợpkhông đi qua tâm O của mặt cầu, ta gọi d là khoảng cách từ tâm O đến đường thẳng, khi đó:

– Nếu d<r, đường thẳngcắt mặt cầu tại hai điểm M, N;
– Nếu d=r, đườnggiác tiếp xúc với mặt cầu tại điểm H, H gọi là tiếp điểm và đường thẳnggọi là tiếp tuyến của mặt cầu.
– Nếu d>r, đường thẳngkhông cắt mặt cầu.

4. Mặt cầu ngoại tiếp một hình đa diện

Một mặt cầu đi qua mọi đỉnh của một hình đa diện H, và hình đa diện H gọi là nội tiếp trong mặt cầu đó.

a. Bất kì hình tứ diện nào cũng có mặt cầu ngoại tiếp.

Xét hình tứ diện ABCD. Gọi A là trục của đường tròng ngoại tiếp. Gọilà trục của đường tròn ngoại tiếpBCD và (P) là mặt trung trực của cạnh AB, thì tâm O của mặt cầu ngoại tiếp ABCD là giao điểm của và (P).

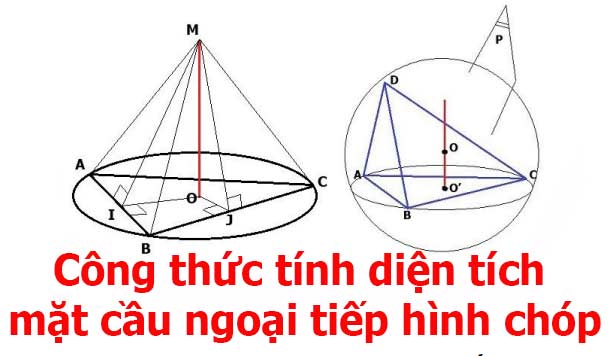
b. Hình chóp S.A1A2…An có mặt cầu ngoại tiếp khi và chỉ khi đáy A1A2…An có đường tròn ngoại tiếp. Tâm của mặt cầu ngoại tiếp hình chóp là giao điểm trục của đường tròn ngoại tiếp đa giác A1A2…An và mặt trung trực một cạnh bên của hình chóp.

c. Hình lăng trụ A1A2…An có mặt cầu ngoại tiếp khi và chỉ khi là hình lăng trụ đứng và dáy có đường tròn ngoại tiếp. Gọi I và I’ lần lượt là tâm hai đáy (tâm đường tròn ngoại tiếp), thì tâm mặt cầu ngoại tiếp của hình lăng trụ là trung điểm O của đoạn thẳng II’.

5. Mặt cầu nội tiếp hình đa diện

Nếu có một mặt cầu (S) tiếp xúc với tất cả các mặt của một hình đa diện H thì ta nói (S) là mặt cầu nội tiếp trong hình đa diện H và H gọi là hình đa diện ngoại tiếp (S)

6. Diện tích mặt cầu và thể tích khối cầu.

Bài tập áp dụng Công thức tính diện tích mặt cầu ngoại tiếp hình chóp

Bài tập 1: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D, AB = AD = a. CD=2a. Cạnh bên SD vuông góc với mặt đáy và SD = a. Gọi E là trung điểm của DC. Tính diện tích mặt cầu ngoại tiếp hình chóp S.BCE.

Bài giải

Từ ABCD là hình thang vuông tại A và D, AB=AD=a, CD=2a suy ra tam giác BEC vuông cân đỉnh E.

Gọi M là trung điểm BC thì M là tâm đường tròn ngoại tiếp tam giác BEC. Do đó, trục đường tròn ngoại tiếp tam giác BEC là đường thẳng đi qua M và vuông góc với mặt phẳng (ABCD). Khi đó //SD.

Gọi (α) là mặt phẳng trung trực của SC và I là giao điểm của (α) vàthì I là tâm mặt cầu (S) ngoại tiếp hình tròn S.BCE
Ta thấy rằng tam giác DBC vuông cân tại B và nên

Bài tập số 2: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Mặt cầu ngoại tiếp hình chóp này có diện tích tính theo a là:

A. πa²                         B. 2πa²                        C. 3. πa²                     D. 4πa²

Gợi ý giải

Kẻ đường sao cho SH của hình chóp thì H là tâm của đáy ABCD.

Ta có SA=SC=a. AC = .Suy ra, AC²=SA²+SC²=2a².

Do đó, SAC vuông tại S.

Chứng minh tương tự, SBD vuông tại S.

Ta được HA=HB=HC=HD=HS=

Do vậy, mặt cầu ngoại tiếp hình chóp S.ABCD có tâm là H và bán kính R=

Diện tích của mặt cầu này là S=4πR² = 4π=2πa².

Bài tập số 3. . Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với mặt phẳng (ABC) và cạnh SA=AB=10cm. Diện tích mặt cầu ngoại tiếp hình chóp bằng:
A. 12πdm            B.  1200πdm              C.1200πdm           D. 12πdm²

Bài giải