Lý thuyết chung về con lắc đơn và các đại lượng đặc trưng

I/ Lý thuyết về con lắc đơn

1/ Cấu tạo con lắc đơn.

Con lắc đơn bao gồm vật nặng có kích thước nhỏ và khối lượng m được treo vào 1 sợi dây có chiều dài là l, có khối lượng không đáng kể và không dãn. Vật nặng có kích thước rất nhỏ so hơn với chiều dài của sợi dây.

2/ Hoạt động:

Kích thích vật m sao cho dây treo vật m hợp với phương thẳng đứng 1 góc α rồi buông tay. Khi đó dưới tác dụng của trọng lực thì vật m chuyển động về VTCB ban đầu (vị trí góc α=0^o), khi vật m đến VTCB do quán tính thì vật m tiếp tục chuyển động sang bên trái, nếu ta bỏ qua sức cản của không khí thì vật sẽ chuyển động đến 1 vị trí sao cho dây treo hợp lúc này với phương thẳng đứng 1 góc là α. Khi đó vật m sẽ dừng lại và chuyển động ngược lại VTCB, chuyển động này được lặp đi lặp lại qua VTCB  => Vậy vật m dao động xung quanh VTCB.

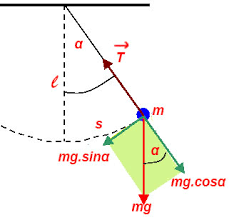
3/ Dao động của con lắc đơn là dao động điều hòa

• Ta có độ dài quãng đường vật m chuyển động từ vị trí của góc hợp với dây treo và phương thẳng đứng là góc α về VTCB (α = 0) là s.
• Để chứng minh được điều này ta cần sử dụng các công thức gần đúng của toán học do góc α rất nhỏ nên ta có sin α ≈ α (α tính theo rad)
• Vậy muốn con lắc đơn dao động điều hòa thì góc α phải rất là nhỏ, thông thường người t coi α < 10º
• Để chứng minh con lắc đơn là dao động điều hòa ta dùng phương pháp động lực học.
• Ta có các lực tác dụng lên vật m gồm trọng lực  và lực căng của dây .

• Theo định luật II Newton ta có:
• Chiếu phương trình (*) lên phương tiếp tuyến của Ot, ta có:
• – Pt = – Psina = ma (1)
• Vì góc α rất nhỏ nên ta có:
• sin α ≈ α = OA / l = s/ l
• Từ (1) ta có:
• – mg.(s / l) = ma ⇔ a = -(g / l).s
• Ta đặt w = g / l và a = s” ta có: s” = – w.s
• =>  s” + w.s = 0
• Giải phương trình này ta có nghiệm của s = S₀ sin(ωt + φ) tương tự phương trình x = A sin(ωt + φ) hoặc nghiệm là s = S₀ cos(ωt + φ) tương tự phương trình x = A cos(ωt + φ) với s giữ vai trò như x và S₀ như A và g/l tương đương k / m
• Vậy ta có với góc α< 10º ta có dao động của con lắc đơn là dao động điều hòa với tần số góc là: 
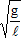
• Nếu góc α > 10º thì dao động của con lắc đơn là dao động tuần hoàn

Chú ý: Các phương trình dao động của con lắc đơn

• s = S₀ cos(ωt + φ) viết theo li độ dài
• α = α₀ cos(ωt + φ) viết theo li độ góc Trong đó ta có: s = α l, S₀ = α₀ l

=> v = s’ = -ωS₀ sin(ωt + φ) = -ωlα₀ sin(ωt +φ)

=>  a = v’ = -ω²S₀ cos(ωt +φ) = -ω²lα₀ cos(ωt + φ) = -ω²s = -ω²αl

4/ Tần số và chu kỳ của con lắc đơn

Tần số góc: ω = 

Chu kỳ con lắc đơn: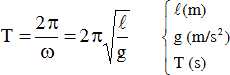 

Chú ý: Khi con lắc đơn dao động tại 1 nơi cố định (có g không đổi), Trong các dao động nhỏ (α ≤ 100). thì ta có chu kỳ dao động của con lắc đơn là T = const, nó không phụ thuộc m, α và tỉ lệ với , những nó tỉ lệ nghịch thì khi đó dao động của con lắc đơn được coi dao động tự do.

Tần số: f = 1/T

5/ Các năng lượng của con lắc đơn

+ Động năng của con lắc đơn: W_đ =  mv².

+ Thế năng: W_t = mg l (1 – cosa) =  mg l a² (a ≤ 10⁰, a (rad)).

+ Cơ năng của con lắc đơn: W = W_t + W_đ = mg l (1 – cosa₀) =  mg l α₀²

Trong khi dao động cơ năng của con lắc đơn sẽ được bảo toàn nếu ta bỏ qua ma sát.

II/ Sự chuyển hóa năng lượng của con lắc đơn

– Kích thích vật m lệch khỏi VTCB một góc α₀ ta đã thực hiện được 1 công và vật m nhận được 1 thế năng.

– Khi mà lực kéo mất, khi lực thành phần tiếp tuyến  của trọng lực  làm vật m chuyển động nhanh dần về VTCB. Ta có thế năng tăng còn động năng giảm.

– Khi vật đến VTCB, thì lực thành phần  = 0, W_t = 0 và W_đ đạt cực đại.

– Do quán tính, vật m tiếp tục đi lên chậm dần vì lúc này  lại xuất hiện nhưng có chiều ngược chiều chuyển động.

– Khi vật m dừng lại (ở biên), ta có W_t  đạt cực đại và W_đ  = 0.

– Quá trình này được lập lại ngược chiều trước và cứ như thế diễn biến: Vậy khi động năng tăng 1 lượng bao nhiêu thì thế năng giảm đi 1 lượng bấy nhiêu và ngược lại như vậy.

III/ Các trường hợp đặc biệt của con lắc đơn

1/ Hệ thức độc lập của con lắc đơn

Ta có : a = -ω²s = -ω²αl 

Trong đó : S= l .α  là hệ thức liên hệ giữa độ dài cung với bán kính cung.

S₀² = S² + (v / w)² Trong đó ta có S₀ biên độ cung tương đương với A

α₀² = α² + v² / w² l²  = α² + v² / gl

2 / Ghép nối 2 con lắc đơn

Xét cùng 1 nơi con lắc đơn chiều dài l₁ có chu kỳ T₁ và con lắc đơn chiều dài l₂ có chu kỳ T₂, ta có:

+ Khi con lắc đơn có chiều dài là l₁ + l₂ có chu kỳ là: T² = T₁² +  T₂²

+ Khi con lắc đơn có chiều dài l₁ – l₂ (trong đó l₁>l₂) có chu kỳ là: T² = T₁² –  T₂²

3/ Trường hợp con lắc đơn dao động với a₀ bất kỳ.

• Cơ năng con lắc đơn: W = mgl(1-cosa₀).
• Vận tốc là: 
• Lực căng của sợi dây khi đó: T = mg(3cosα – 2cosα₀)
• Chú ý:  Các công thức này được áp dụng đúng cả khi mà a₀có giá trị lớn
• Khi con lắc đơn là dao động điều hoà (a₀<< 1rad) thì ta có:
• W = ½ mgl α₀²
• v² = gl (α₀² – α² )

Ta có: T = mg (1 + α₀² – 3/2. α²)

Kết luận:

• Khi con lắc đi qua VTCB (α = 0) thì khi đó ta có tốc độ và lực căng dây đều đạt giá trị là lớn nhất:

Và Tmax = mg (3 – 2cosα₀)

• Khi con lắc đơn đi qua vị trí biên (α = α0) thì khi đó ta có tốc độ và lực căng dây đều có giá trị nhỏ nhất:

Và Tmin = mg (3 cosα₀ – 2 cosα₀) = mg cosα₀

4/ Trường hợp 4:

Khi con lắc đơn có chu kỳ T ở độ cao là h₁ và có  nhiệt độ t₁. Đưa con lắc đơn tới độ cao là h₂ và nhiệt độ là t₂ thì ta có:

ΔT / T = Δh / R + αΔt / 2

     Trong đó R = 6400km là bán kính Trái Đât, α là hệ số nở dài của con lắc.