Trong chương trình vật lý lớp 12 thì chuyên đề về con lắc đơn là không thể thiếu trong các bài ôn thi trung học phổ thông cũng như đại hỏi. Các bài tập con lắc đơn sau đâu sẽ giúp bạn có thêm kỹ năng để giải bài tập nhanh và chính xác hơn
I/ Bài tập con lắc đơn có lời giải
Bài 1: Cho 1 con lắc đơn dao động điều hoà có phương trình li độ góc là α = 0,1cos(2πt + π/4) ( rad). Trong 1 khoảng thời gian là 5,25s tính từ lúc con lắc bắt đầu quá trình dao động, hỏi có bao nhiêu lần con lắc đó có độ lớn vận tốc là bằng 1/2 vận tốc cực đại?
- 11 lần.
- 21 lần.
- 20 lần.
- 22 lần.
 Giải:
Giải:
Ta có trong 1 chu kì dao động thì có 4 lần:
v = vmax / 2 tại vị trí là Wđ = ¼ W
=> Wt = ¾ Wtmax khi đó ta có li độ
α = ± ![]()
Ta có chu kì của con lắc đơn là: T = 2 π /ω= 1 (s)
- Với t = 5,25 (s) = 5T + ¼ T
- Với t = 0 => α0 = 0,1 cos(π/4) =
 ; khi đó vật sẽ chuyển động theo chiều âm về vị trí cân bằng
; khi đó vật sẽ chuyển động theo chiều âm về vị trí cân bằng
Sau khi vật thực hiện 5 chu kì vật sẽ trở lại vị trí ban đầu và sau T/4 tiếp theo vật chưa qua vị trí α = – ![]()
Do đó: Ta có trong khoảng thời gian 5,25s tính từ lúc con lắc bắt đầu quá trình dao động thì con lắc có độ lớn vận tốc là bằng 1/2 vận tốc cực đại là 20 lần.
Đáp án C
Bài 2: Cho 1 con lắc đơn có chiều dài là l = 64cm, có khối lượng m = 100g. Kích thích con lắc lệch khỏi VTCB 1 góc là 6° rồi thả nhẹ cho nó dao động. Sau 20 chu kì ta có biên độ góc còn là 3º. Lấy g= 2π = 10m/s2. Để cho con lắc dao động với biên độ góc 60 thì ta phải dùng bộ máy đồng hồ bổ sung năng lượng cho con lắc có công suất trung bình là bao nhiêu
- 0,77mW.
- 0,082mW.
- 17mW.
- 0,077mW
Giải bài tập con lắc đơn:
Ta có α0 = 6º = 0,1047rad.
Cơ năng ban đầu của con lắc là W0 = mgl (1 – cosα0) = 2 mgl sin2 (α0 / 2) ≈ mgl (α02 / 2)
Ta có cơ năng sau khoảng thời gian t = 20T: W = mgl(1- cosα) = 2mgl sin2 (α/2) ≈ mgl (α2/2) = mgl (α02/8)
Cơ năng sau 20 chu kì giảm: ∆W = mgl ((α02 / 2) – (α02 / 8) = mgl (3α02 / 8) = 0,00263 J
Theo công thức của T ta có T = 1,6 (s)
Vậy công suất trung bình ta cần cung cấp để con lắc tiếp tục dao động duy trì với biên độ góc là 6
WTB = ∆W / T = 2,63.103 / 32 =0,082.10-3 = 0,082mW.
Đáp án B
Bài 3: Cho 1 sợi dây chiều dài l , và được cắt ra làm 2 đoạn l1,l2 , để dùng làm 2 con lắc đơn. Cho biết li độ của con lắc đơn có chiều dài l1 ( trong trường hợp động năng bằng thế năng) có giá trị bằng li độ của con lắc đơn có chiều dài l2 (trong trường hợp động năng bằng hai lần thế năng). Biết vận tốc cực đại của con lắc đơn l1 bằng 2 lần vận tốc cực đại của con lắc đơn l2. Tính chiều dài l ban đầu.
Giải:
Giả sử ta có phương trình dao động của con lắc đơn có dạng là α = α0cosωt
Cơ năng của con lắc đơn tại thời điểm có li độ α là
W= mv2/2 + mgl(1- cosα) = mgl(1- cosα0).
Ta có Wt = mgl(1- cosα) = mgl .2sin2(α/2) ≈ mgl.2α2/4= mgl(α2/2) ;
Ta có W = W0 = mgl(α02/2)
Với con lắc l1:
Khi Wđ = Wt Ta có α12 = α012/2;
Với con lắc l2
Khi Wđ = 2Wt Ta có α22 = α022 /3
Ta có α1 = α2 => 
Khi đó vận tốc cực đại của con lắc đơn là vmax = ωlα0 = ![]()
Ta có v1max = 2v2max => gl1 α012 = 4gl2 α022 => l1 α012 = 4l2 α022 (**)
Từ (*) và (**) ta có ![]()
Bài 4: Treo 1 vật trong lượng là 10N vào 1 đầu sợi dây nhẹ, không co dãn. Kéo vật khỏi phương thẳng đứng 1 góc α0 rồi thả nhẹ cho vật đó dao động. Biết rằng dây treo chịu được lực căng lớn nhất 20N. Để cho dây không bị đứt thì góc α0 không thể vượt quá bao nhiêu độ
:A: 15º. B:30º. C: 45º. D: 60º.
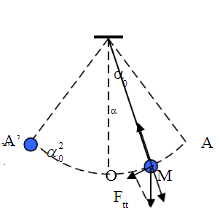 Giải
Giải
Xét thời điểm khi vật ở vị trí M, góc lệch của sợi dây treo là α
Vận tốc của vật tại vị trí M là: v2 = 2gl( cosα – cosα0).
Ta có lực căng của dây treo khi vật ở vị tri M:
T = mg cosα + mv2/ l = mg (3cosα – 2cosα0).
Ta có T = Tmax khi α = 0
- Tmax = P(3 – 2cosα0) = 10(3 – 2cosα0) ≤ 20 => 2cosα0 ≥ 1 => cosα0 ≥ 0,5
- α0 ≤ 60º .
Đáp án D
Bài 5: 1 con lắc đơn gồm một vật nhỏ được treo vào đầu dưới của một sợi dây không dãn và đầu trên của sợi dây được gắn cố định. Ta bỏ qua ma sát lực cản của không khí. Ta kéo con lắc lệch khỏi vị trí phương thẳng đứng 1 góc 0,1rad rồi sau đó thả nhẹ. Tính tỉ số độ lớn gia tốc của vật tại vị trí cân bằng và độ lớn gia tốc của vật tại vị trí biên
: A: 0,1. B: 0. C: 10. D: 1
Giải bài tập con lắc đơn:
Xét tại thời điểm khi vật ở M, ta có góc lệch của dây treo là α
Khi dó vận tốc của vật tại vị trí M
v2 = 2gl( cosα – cosα0) => ![]()
ta có: ![]()
Gia tốc hướng tâm
aht = v2 / l= 2g(cosα – cosα0) => att = Ftt / m = Psinα / m = gα
Tại vị trí cân bằng ta có: α = 0 => att = 0 nên a0 = aht = 2g(1 – cosα0) = 2g.2 sinα02 / 2 = g α02
Tại vị trí biên : α = α0 nên aht =0 —-> aB = att = gα0
Do đó :a0 / aB = g α02 / g α0 = α0 = 0,1 .
Đáp án A
II/ Bài tập con lắc đơn không có lời giải
1/ Trắc nghiệm bài tập con lắc đơn
Bài 1: Cho 1 con lắc đơn có chiều dài là l= 40cm, treo tại nơi có g = 10m/s2. Ta bỏ qua sức cản của không khí. Đưa con lắc lệch khỏi vị trí cân bằng 1t góc là 0,1rad rồi truyền cho vật m 1 vận tốc 20cm/s theo phương vuông góc với dây và hướng về vị trí cân bằng. Ta chọn gốc tọa độ tại VTCB của vật nặng và gốc thời gian là lúc gia tốc của vật m tiếp tuyến với quỹ đạo lần thứ 1.
Hãy viết phương trình dao động của con lắc theo li độ cong
- 8cos(25t +π) cm
- 42cos(25t +π) cm
- 42cos(25t +π/2) cm
- 8cos(25t) cm
Bài 2: Cho 1 con lắc đơn gồm vật có khối lượng m và dây treo có chiều dài l = 2m, lấy g = π2. Cho con lắc dao động điều hòa dưới tác dụng của 1 ngoại lực có biểu thức là F = F0cos(ωt + π/2) N. Nếu chu kỳ T của ngoại lực này tăng từ 2s lên 4s thì ta có biên độ dao động của vật sẽ thay đổi như thế nào:
A tăng rồi giảm B chỉ tăng C chỉ giảm D giảm rồi tăng
Bài 3: Cho 1con lắc đơn dao động ở trong môi trường không khí. Ta kéo con lắc lệch theo phương thẳng đứng 1 góc 0,1 rad rồi thả nhẹ. Biết rằng lực căn của không khí đã tác dụng lên trên con lắc là không đổi bằng 0,001 lần trọng lượng vật.Ta coi biên độ giảm đều trong từng chu kỳ dao động, số lần con lắc dao động qua vị trí cân bằng cho đến lúc dừng lại là:
A: 25 B: 50 C: 100 D:
Bài 4: 1 con lắc lò xo treo thẳng đứng và 1 con lắc đơn đã được tích điện q, có cùng khối lượng m. Trong môi trường không có điện trường chúng dao động điều hòa với cùng chu kỳ là T1 = T2. Ta đặt cả 2 cong lắc trong cùng 1 điện trường đều có véc tơ cường độ điện trường là E nằm ngang thì ta có độ giãn của con lắc lò xo tăng lên 1,44 lần, còn con lắc đơn dao động với chu kỳ 5/6 s. Tìm chu kì dao động của con lắc lò xo này trong điện trường đều là bao nhiêu:
- 5/6 s.
- 1 s.
- 1,44s.
- 1,2s
2/ Bài tập
Bài 1: Cho 1 con lắc đồng hồ được coi là con lắc đơn và có chu kỳ dao động là T = 2 (s). Một vật có khối lượng m = 1kg. Biết rằng biên độ góc ban đầu là . Do vậy chịu tác dụng của 1 lực cản không đổi là Fc = 0,011N nên vật chỉ dao động trong 1 khoảng thời gian rồi dừng lại. Ta dùng 1 pin có hiệu suất 3V điện trở trong của nó không đáng kể để bổ sung cho con lắc với hiệu suất là 25%. Pin có điện lượng là 104 c. Hỏi đồng hồ chạy được thời gian bao lâu thì ta phải thay pin
Bài 2 : Cho 1 con lắc đơn có khối lượng m1 = 400g và có chiều dài 160cm. K vật lệch khỏi vị trí cân bằng 1 góc 600 rồi thả nhẹ cho vật m dao động, khi vật m đi qua vị trí cân bằng vật va chạm mềm với vật m2 = 100g khi m2 đang đứng yên, ta lấy g = 10m/s2. Hỏi biên độ góc của con lắc sau khi va chạm là
Hi vọng với những bài tập con lắc đơn trên có thể giúp các bạn nhiều kiến thức bổ ích hơn. Chúc các bạn làm bài tốt.