– Trong chương trình vật lý lớp 12 chuyên đề về con lắc lò xo là một trong những chuyên đề quan trọng yêu cầu các bạn phải nắm vững kiến thức để có thể giải hết các dạng bài tập về con lắc lò xo.
I/ Các dạng bài tập về con lắc lò xo
+ Xác định các đại lượng đặc trưng của dao động về con lắc lò xo.
+ Tính chiều dài của lò xo trong quá trình con lắc dao động.
+ Tính lực đàn hồi, lực phục hồi (hay lực kéo về) của 1 con lắc lò xo.
+ Tính các loại năng lượng của 1 con lắc lò xo trong quá trình nó dao động.
+ Xác định thời gian lò xo giãn và nén.
+ Khi ta thay đổi khối lượng của vật nặng và mức độ ảnh hưởng của nó đến chu kỳ dao động.
+ các dạng bài tập về cắt ghép lò xo.
– Ngoài ra còn một số dạng bài tập về con lắc lò xo nâng cao chúng ta cũng cần lưu ý như :
+ Dạng bài tập giữ cố định 1 điểm trên lò xo khi lò xo đó đang dao động và tìm biên độ dao động mới của lò xo.
+ Dạng bài tập về kích thích dao động của 1 con lắc lò xo khi va chạm.
+ Xác định dao động của con lắc lò xo trong 1 hệ quy chiếu không quán tính
>> Dạng bài tập m1 được đặt trên m2 và dao động điều hòa theo phương ngang.
>> Một vật m1 được đặt trên vật m2 và có dao động điều hòa theo phượng thẳng đứng.
>> Khi vật m1 và m2 gắn vào hai đầu của lò xo đặt thẳng đứng, m1 dao động điều hòa.
+ … và một số dạng bài tập về con lắc lò xo khác sẽ được liệt kê sau:
II/ Cách giải các dạng bài tập về con lắc lò xo
1/ Dạng bài tập về con lắc lò xo liên quan tới việc xác định các đại lượng đặc trưng.
Sử dụng các công thức liên quan:
- Tần số góc của con lắc lò xo
+ 
+ 
+ 
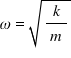
– Chu kỳ dao động:
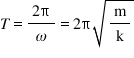
– Tần số dao động:
– Các công thức có liên quan đến biên độ dao động của con lắc lò xo:
+ x và v vuông pha nhau nên ta có hệ thức :
+ 
+
+ 
+ 
+ 
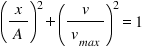
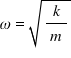
– Các công thức về pha ban đầu φ :
+ Lúc t = 0 thì ta có 
2/ Dạng bài tập liên quan đến chiều dài của lò xo trong quá trình dao động.
– Ta có chiều dài tự nhiên của lò xo là l0.
a) Xác định chiều dài của con lắc lò xo nằm ngang:
+ Lúc vật ở vị trí cân bằng và lò xo không bị biến dạng
+ Ta có chiều dài cực đại của lò xo là: 
+ Ta có chiều dài cực tiểu của lò xo là: 
b) Xác định chiều dài khi con lắc lò xo được bố trí theo phương thẳng đứng hoặc phương nằm nghiêng một góc và được treo ở dưới.
+ Khi đó dộ biến dạng của lò xo khi vật tại vị trí cân bằng: 
+ Chiều dài của lò xo khi vật tại vị trí cân bằng: 
+ Chiều dài của lò xo ở li độ x là: 
+ Ta có chiều dài cực đại của lò xo là: 
+ Ta có chiều dài cực tiểu của lò xo là : 
3/ Dạng bài tập về con lắc lò xo liên quan tới lực đàn hồi và lực phục hồi (lực kéo về).
a) Dạng bài tập về con lắc lò xo liên quan tới lực đàn hồi:
– Mỗi 1 lò xo đều có một chiều dài tự nhiên là lo và có độ cứng xác định k.
– Khi 1 lò xo bị nén hay bị giãn (bị biến dạng) thì mỗi đầu lò xo đều xuất hiện một lực đàn hồi.
– Khi lực đàn hồi này có phương trùng với trục của lò xo và ngược hướng với sự biến dạng, có độ lớn tỉ lệ với độ biến dạng này.
– Ta có công thức tính độ lớn của lực đàn hồi là: 
trong đó ta có . 
+ Nếu l > lo thì lò xo sẽ bị giãn Δl > 0
+ Nếu l < l0 thì lò xo sẽ bị nén Δl < 0
* Nếu như con lắc lò xo được bố trí nằm ngang thì:
+ Tại vị trí cân bằng ta có: x = 0, Fdhmin = 0.
+ Tại vị trí biên ta có: 
* Nếu con lắc lò xo được bố trí theo phương thẳng đứng thì:
+ Ta có lực đàn hồi cực đại là: 
+ Lực đàn hồi cực tiểu của con lắc lò xo là:
>> Trường hợp: 
: thì trong quá trình dao động lò xo luôn giãn 
>> Trường hợp: 
: thì trong quá trình dao động lò xo sẽ bị giãn và bị nén. Khi vật qua vị trí cân bằng lò xo có lực đàn hồi là: 
b) Lực phục hồi của con lắc lò xo:
– Trong dạng bài tập về con lắc lò xo thì lực phục hồi của con lắc lò xo luôn hướng về VTCB trong suốt quá trình lò xo dao động.
– Khi đó công thức tính độ lớn của lực phục hồi là : 
4/ Bài tập về năng lượng của con lắc lò xo trong quá trình dao động.
Ta có các công thức về năng lượng của con lắc lò so sau:
– Động năng của con lắc lò xo: 
– Thế năng của con lắc lò xo: 
– Cơ năng của con lắc lò xo: 
– Tuy rằng cơ năng của con lắc lò xo không thay đổi nhưng động năng, thế năng của con lắc lò xo đều biến thiên với tần số: 
– Tuy nhiên động năng và thế năng của nó biến đổi qua lại cho nhau, khi động năng tăng gấp n lần thế năng 
thì ta có:
Tương tự ngược lại ta có:
– Chú ý: 
biểu thức này sẽ giúp ta tính nhanh động năng của 1 vật khi vật này qua li độ x.
5/ Bài tập về tính thời gian lò xo giãn và nén.
– Trường hợp con lắc lò xo nằm ngang thì ta có thời gian lò xo giãn sẽ bằng thời gian lò xo nén.
– Trường hợp con lắc được bố trí theo phương thẳng đứng hoặc nằm nghiêng khi lò xo được treo ở dưới ta có.
+ Trường hợp 1: 
: Trong quá trình dao động thì lò xo chỉ bị giãn mà không có bị nén. Vậy thời gian lo xo giãn bị sẽ = T và thời gian lò xo bị nén = 0.
+ Trường hợp 2: 
: Khi lò xo bị nén vật có li độ nằm trong khoảng từ 
đến 
(chiều dương hướng lên). Khi đó bài toán sẽ được chuyển thành tìm khoảng thời gian ngắn nhất của vật đi từ vị trí có li độ x1 đến x2.
– Khi đó khoảng thời gian ngắn nhất mà vật đi từ vị trí có li độ 
đến là: 
. Từ đó suy ra thời gian lò xo bị nén trong 1 chu kỳ là: 
– Và khoảng thời gian lò xo bị giãn là : .
6/ Dạng bài tập về con lắc lò xo khi thay đổi khối lượng vật nặng và nó ảnh hưởng đến chu kỳ của dao động.
– Khi ta gắn 1 vật có khối lượng m1 thì khi đó con lắc có chu kỳ là T1.
– Khi ta gắn 1 vật có khối lượng m2 thì khi đó con lắc có chu kỳ T2.
– Khi ta gắn 1 vật có khối lượng 
thì khi đó con lắc có chu kỳ thay đổi theo công thức là:
+ Đối với trường hợp tương tự ta có: 
: 
7/ Dạng bài tập về cắt ghép lò xo:
Đây là một dạng bài tập về con lắc lò xo khá phức tạp chúng ta cần xét trường hợp sau:
a) Trường hợp ghép lò xo:
+ Trường hợp 1: ghép nối tiếp 2 lò xo: 
thì ta có: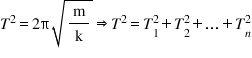 
+ Trường hợp 2: ghép song song 2 lò xo: 
thì ta có: 
b) Trường hợp cắt lò xo:
Nếu các lò xo có độ cứng lần lượt k1, k2,…,kn và có chiều dài tự nhiên là l1, l2, …ln có cùng bản chất giống nhau (hoặc được chúng cắt từ lò xo ban đầu là k0, l0) thì ta có 
.
+ Nếu biết k0 của 1 lò xo có chiều dài ban đầu là l0 thì ta có thể tìm được k’ của 1 đoạn lò xo l’ được cắt ra từ lò xo đó theo biểu thức sau: 
8/ Dạng bài tập giữ cố định 1 điểm trên lò xo khi lò xo đó đang dao động và tìm biên độ dao động mới của lò xo đó.
– Khi đó ta có cơ năng sau bằng cơ năng ban đầu trừ đi phần thế năng bị mất do đoạn lò xo bị giữ : 
– Nếu
+ l là khoảng cách từ vị trí gốc đến điểm cố định trên lò xo.
+ l0 là chiều dài của con lắc lò xo.
– Tính phần thế năng bị mất theo các bước sau:
+ Ta tính k’ theo công thức’: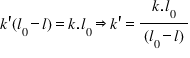 
+ Tiếp theo ta cần tính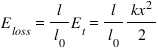 
+ Ta tính tiếp E’: 
+ Từ đó suy ra A’: 
+ Nếu ta đặt 
thì ta có 
9/ Dạng bài tập kích thích dao động của một con lắc lò xo bằng va chạm.
– Dạng bài tập về con lắc lò xo khi bắn một vật m0 với 1 vận tốc v0 vào vật M được gắn với lò xo. Ta có 2 dạng va chạm là va chạm mềm và va chạm đàn hồi.
a) Trường hợp va chạm đàn hồi:
– Định nghĩa: Va chạm đàn hồi là va chạm mà sau khi va chạm 2 vật tách rời nhau ra và chuyển động với 2 vận tốc khác nhau. Chúng ta cân nghiên cứu về loại va chạm đàn hồi xuyên tâm: là loại va chạm mà sau khi va chạm cả 2 vật tách rời nhau nhưng cùng chuyển động trên một đường thẳng.
– Trong loại va chạm này thì tổng động lượng và động năng của hệ đều được bảo toàn nên:
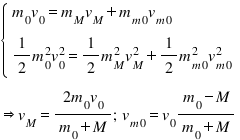
b) Trường hợp va chạm mềm:
Định nghĩa: là loại va chạm mà sau khi va chạm 2 vật dính vào nhau và cùng chuyển động với cùng 1 vận tốc. Trong va chạm mềm này thì tổng động lượng của hệ được bảo toàn nên ta có:
10/ Bài tập khi m1 đặt trên m2 cùng dao động điều hòa theo phương ngang.
– Gọi hệ số ma sát giữa m1, m2 là . Ta bỏ qua ma sát giữa vật m2 và mặt sàn. Xác định điều kiện của biên độ A để vật m1 không trượt trên m2 trong quá trình vật dao động.
– Để có vật m1 không bị trượt ta có: 
11/ Khi vật m1đặt trên vật m2và dao động điều hòa theo phượng thẳng đứng.
– Dạng bài tập về con lắc lò xo khi để vật m1 luôn nằm yên trên vậy m2 trong quá trình dao động thì ta có: 
12/ Khi vật m1 và m2 được gắn vào 2 đầu của lò xo đặt thẳng đứng và m1 dao động điều hòa.
– Để vật m2 luôn nằm yên trên mặt sàn trong quá trình vật m1 dao động thì ta có: 
Trên đây là một số dạng bài tập về con lắc lò xo thường gặp và phương pháp giải các bài tập này, hi vọng giúp ích cho các bạn học sinh trong quá trình ôn luyện kiến thức
