Toán học luôn phong phú và đa dạng với nhiều dạng toán từ đơn giản cho đến phức tạp đòi học chúng ta phải tư duy cũng như phải ghi nhớ các công thức để có thể áp dụng vào giải toán. Để cũng cố thêm cũng như giúp các bạn tìm kiếm công thức nhanh nhất khi cần hôm nay chúng tôi xin gửi tới bạn công thức tính delta và giải phương trình bậc 2 delta phẩy hay nhất. Mong rằng sẽ giúp ích được cho các bạn trong công cuộc học tập vất vả này.
Bài viết hôm nay chúng ta sẽ cùng nhau hệ thống lại Công thức tính đelta và đenlta phẩy giải phương trình bậc 2 cũng như hệ thống viet và một số bài tập để các bạn tự giải.
I . Phương trình bậc 2 là gì? Công thức nghiệm phương trình bậc 2?
Phương trình bậc 2 là phương trình có dạng:
ax2 + bx +c = 0
Trong đó: a ≠ 0 , a , b là hệ số, c là hằng số
Công thức nghiệm:
Ta xét phương trình
ax2 + bx +c = 0
CÔNG THỨC TÍNH DELTA :
Δ = b2 – 4ac
Sẽ có 3 trường hợp:
+ Δ < 0 => Phương trình vô nghiệm (vì đây là căn bậc 2)
+ Δ = 0 => x = – b/2a (giá trị rút gọn phân số)
+ Δ > 0 => x c {- b + √Δ/2a ; – b – √Δ/2a}
Ví dụ: Cho phương trình x2 + 4x – 2 = 0 . Tìm nghiệm của phương trình bậc 2 trên
Trước hết tính detla Δ = b2 – 4ac = 4*4 – 4*2*1 = 8 .
Vì Δ = 8 > 0 nên phương trình sẽ có 2 nghiệm phân biệt là:
X1 = (-4 – √8 ) / 2
X2 = (-4 + √8 ) / 2
CÔNG THỨC TÍNH DELTA PHẨY:
Δ’ = b’2 – ac
+ Δ’ < 0 => Phương trình vô nghiệm (vì đây là căn bậc 2)
+ Δ’ = 0 => x = – b’/a (giá trị rút gọn phân số)
+ Δ’ > 0 => x = {(- b’ + √Δ’)/a ; (- b’ – √Δ’) /a}
Công thức này được gọi là công thức nghiệm thu gọn
Ví dụ: Cho phương trình x² – 2(m+1)x + m² + m +1 = 0
a . Tìm các giá trị của m để phương trình có nghiệm
b . Trong trường hợp phương trình có nghiệm là x1, x2 hãy tính theo m :
x1+ x2 ; x1* x2 ; (x1)² +( x2)²
Đáp số:
a . Δ′ = m + 2 >= 0 khi m >= -2
b . x1 + x2 = 2(m +1)
x1 * x2 = m² + m – 1
(x1)² + (x2)² = (x1 + x2)² – 2 (x1* x2)
= 4m² + 8m +4 – 2m² – 2m + 2
= 2m² + 6m +6
Hệ thức Viet
Nếu ta có x1, x2 là nghiệm của phương trình: ax2 + bx +c = 0
thì: x1; x2: S = x1 + x2 = -b/a
P = x1 . x2 = c/a
II . Bài tập vận dụng công thức tính đelta và đental phẩy phương trình bậc 2
Bài 1: Cho phương trình
a) Chứng minh rằng phương trình luôn có nghiệm với mọi k.
b) Tìm k để phương trình có hai nghiệm cùng dấu. Khi đó hai nghiệm mang dấu gì?
c) Tìm k để phương trình có tổng hai nghiệm bằng 6. Tìm hai nghiệm đó.
Giải:
a) Phương trình đã cho là phương trình bậc hai.

Bài 2. Cho phương trình:

Bài 3: Gọi m và n là các nghiệm của phương trình

Hiển nhiên m, n đều khác -1 và -1 không thoản mãn phương trình (1).
Ta có:
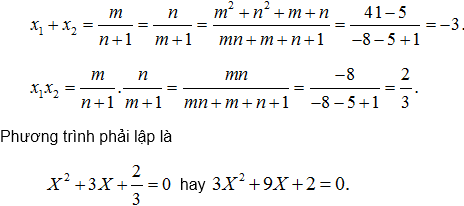
Bài 4:
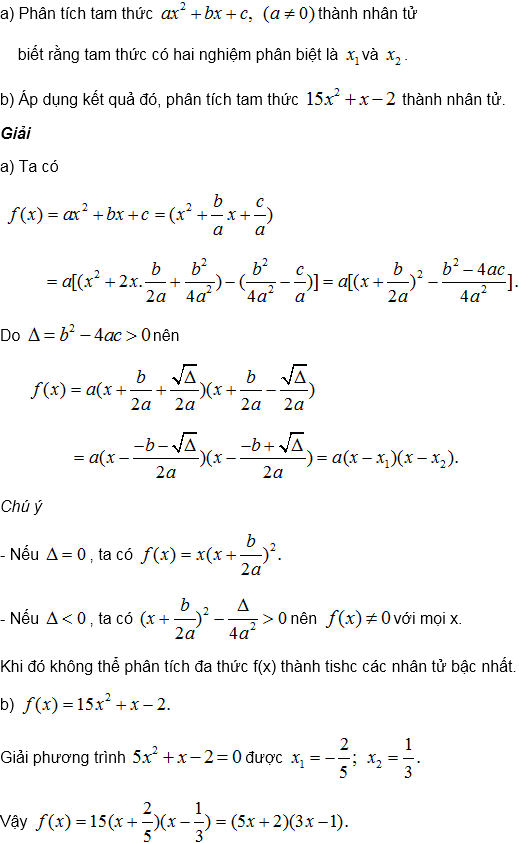
III . Bài tập tự giải vận dụng công thức tính đelta và đental phẩy phương trình bậc 2
Bài 1: Chứng minh rằng phương trình sau có nghiệm với mọi a ; b :
(a+1) x² – 2 (a + b)x + (b- 1) = 0
Bài 2: Giả sử phương trình bậc hai x² + ax + b + 1 = 0 có hai nghiệm dương. Chứng minh rằng a² + b² là một hợp số.
Bài 3: Cho phương trình (2m – 1)x² – 2(m + 4 )x +5m + 2 = 0 (m #½)
- Tìm giá trị của m để phương trình có nghiệm.
- Khi phương trình có nghiệm x1, x2, hãy tính tổng S và tích P của hai nghiệm theo m.
- Tìm hệ thức giữa S và P sao cho trong hệ thức này không có m.
Bài 4: Cho phương trình x² – 6x + m = 0. Tính giá trị của m, biết rằng phương trình có hai nghiệm x1, x2 thỏa mãn điều kiện x1 – x2 = 4.
Bài 5: Cho phương trình bậc hai: 2x² + (2m – 1)x +m – 1 =0
- Chứng minh rằng phương trình luôn luôn có nghiệm với mọi m.
- Xác định m để phương trình có nghiệm kép. Tìm nghiệm đó.
- Xác định m để phương trình có hai nghiệm phan biệt x1, x2 thỏa mãn -1<x1< x2<1
- Trong trường hợp phương trình có hai nghiệm phân biệt x1, x2, hãy lập một hệ thức giữa x1, x2 không có m.
Bài 6. Cho f(x) = x² – 2(m +2)x+ 6m +1
- Chứng minh rằng pt f(x) = 0 luôn nghiệm với mọi m.
- Đặt x = t + 2; tình f(x) theo t. Từ đó tìm điều kiện của m để phương trình f(x) = 0 có hai nghiệm phân biệt lớn hơn 2.
Bài 7: Cho tam thức bậc hai f(x) = ax² + bx +c thỏa mãn điều kiện Ι f(x)Ι =< 1 với mọi x ∈ { -1; 1 }. Tìm GTNN của biểu thức A= 4a² + 3b².
Bài 8: Cho phương trình (x²)² – 13 x² + m = 0. Tìm các giá trị của m để phương trình:
- Có bốn nghiệm phân biệt.
- Có ba nghiệm phân biệt.
- Có hai nghiệm phân biệt.
- Có một nghiệm
- Vô nghiệm.
Trên đây là bài viết giới thiệu về phương trình bậc 2 và công thức tính delta, đenlta phẩy và các bài tập áp dụng công thức đenlta để các bạn tham khảo và luyện tập.
Mong rằng bạn sẽ chăm chỉ luyện tập và dành được kết quả cao trong học tập và thi cử nhé. Mọi cố gắng của bạn sẽ được đền đáp xứng đáng nếu như bạn chăm chỉ và cần mẫn. Chúc các bạn thành công !









