Xét sự đồng biến nghịch biến của hàm số y = f(x) trên 1 khoảng nhất định thực chất là chúng ta xét dấu của đạo hàm y’ trên khoảng đó.
I/ Khái niệm sự đồng biến nghịch biến của hàm số
Ta kí hiệu K là 1 khoảng hay 1 nửa khoảng hoặc 1 đoạn
a) Một hàm số f(x) gọi là đồng biến trên K nếu như với mọi cặp x1, x2 ∈ K mà x1 < x2 thì f(x1) < f(x2)
b) Một hàm số f(x) gọi là nghịch biến trên K nếu như với mọi cặp x1, x2 ∈ K mà x1 < x2 thì f(x1) > f(x2)
Một hàm số f(x) đồng biến ( hay nghịch biến ) trên K còn được gọi là tăng ( giảm ) trên K. Hàm số f(x) đồng biến hay nghịch biến trên K còn được gọi chung là hàm số f(x) đơn điệu trên K
II/ Định lý
1/ Định lý sự đồng biến nghịch biến của hàm số
Giả sử 1 hàm số f(x) có đạo hàm trên khoảng K
a) Nếu đạo hàm f′(x) > 0 với mọi x ∈ K thì ta có hàm số f(x) luôn đồng biến trên khoảng K
b) Nếu đạo hàm f′(x) < 0 với mọi x ∈ K thì ta có hàm số f(x) luôn nghịch biến trên khoảng K
c) Nếu đạo hàm f′(x) = 0 với mọi x ∈ K thì ta có hàm số f(x) luôn không đổi trên khoảng K
Chú ý:
Trong khoảng K ở trong định lý trên ta có thể được thay bằng 1 đoạn hoặc 1 nửa khoảng khi đó ta phải bổ sung giả thiết hàm số f(x) liên tục trên đoạn nửa khoảng đó
Ví dụ : Nếu hàm số f(x) liên tục trên [a;b] và có đạo hàm f′(x) > 0 trên (a;b) thì hàm số f(x) luôn đồng biến trên đoạn [a;b].
Người ta có thể diễn đạt điều này qua bảng biến thiên:
 Việc chúng ta tìm sự đồng biến nghịch biến của hàm số còn được gọi là xét chiều biến thiên của 1 hàm số.
Việc chúng ta tìm sự đồng biến nghịch biến của hàm số còn được gọi là xét chiều biến thiên của 1 hàm số.
Qua định lý trên ta thấy việc xét chiều biến thiên của 1 hàm số có đạo hàm ta có thể chuyển về việc xét dấu đạo hàm của hàm số đó.
2/ Định lý về dấu tam thức bậc 2
Cho hàm số f(x) = ax2 + bx + c với a ≠ 0 có ∆ = b2 – 4ac ta có
- Nếu ∆ < 0 thì ta có f(x) cùng dấu với a với mọi x ∈ R
- Nếu ∆ = 0 thì ta có f(x) cùng dấu với a với mọi x ≠ -b/2a
- Nếu ∆ > 0 thì ta có f(x) = 0 có hai nghiệm là x1, x2 với x1 < x2 ta có

Chú ý: Cho hàm số f(x) = ax2 + bx + c với a # 0 thì ta có
f(x) ≥ 0 với mọi x khi và chỉ khi a > 0 và ∆ ≤ 0
f(x) ≤ 0 với mọi x khi và chỉ khi a < 0 và ∆ ≤ 0
III/ Phương pháp xét sự đồng biến nghịch biến của hàm số
– Bước 1: Ta tìm tập xác định của hàm số và tính f'(x)
– Bước 2: Tìm các điểm mà tại đó ta có f'(x)= 0 hay f'(x) không xác định
– Bước 3: Sắp xếp các điểm này theo thứ tự tăng dần rồi lập bảng biến thiên
– Bước 4: Kết luận về sự đồng biến nghịch biến của hàm số theo định lý
Ví dụ: xét sự đồng biến nghịch biến của hàm số y = (1 / 3)x³ – 3x² + 8x – 2
ta có tập xác đinh D = R
y’ = x² – 6x + 8 với y’ = 0 thì x = 2 và x = 4
Ta có bảng xét dấu
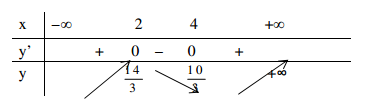
Vậy ta có hàm số đồng biến trên (-∞ ; 2) và (4 ; ∞) nghịch biến trên (2 ; 4)